이번 포스팅에서는 불균형 데이터를 다루는 방법 중 샘플링하는 기법들에 집중하여 (그 중에서도 Oversampling 위주로) 정리해보았다. 현실 세계에서 불균형 데이터를 많이 찾아볼 수 있는 만큼 다양한 연구를 찾아볼 수 있는데, 이번 포스팅에서는 SMOTE와 그 변형 방법들 중 일부를 살펴본다. 개념을 정리하면서 Kaggle에서 찾을 수 있는 통신사 이탈률 데이터를 이용하여 비교를 해볼 예정이다.
여기에 정리하지 않은 변형들도 많으며 이처럼 방법론이 다양한 이유는 가장 기본적인 Oversampling과 Undersampling이 극단적인 불균형 데이터에서 아무런 기대 효과를 발휘하지 못하기 때문이다. 흔히 알려진 단점만 나열해보자면 Oversampling은 minority class에 대한 중복 데이터가 많아지므로 모델이 train셋에 있는 minority class에 과적합되어 test셋에서는 성능을 발휘하지 못한다는 점이 첫번째이다. 다음으로 Undersampling은 주어진 데이터의 일부를 사용하지 않는 것으로 마찬가지로 small sample이 가지는 우려와 더불어 정보를 버리게된다는 단점이 있다. 이러한 점을 해결하기 위해 Oversampling에서는 synthetic sample을 generate하는 방법론들이 많이 등장하며, Undersampling에서는 일부를 선택하더라도 데이터를 잘 대표하는 제대로된 관측치를 선택하고자하는 clustering 방법을 가미한 방법론들도 이슈이다.
1. SMOTE: Synthetic Minority Over-sampling Technique
주로 Oversampling에 근간이 되는 SMOTE는 이름 그대로 minority class에서 synthetic 샘플을 생성하는 방법이다. k-nearest neighbors(knn)를 이용한다는 점이 가장 큰 특징으로 먼저 knn으로 가까운 minority class 들을 찾은 후 0과 1사이의 랜덤한 값을 선택한 후 해당 값으로 내분하는 점을 새로운 샘플로 생성하는 기법이다. 즉 minority 관측치들 사이의 linear 상에서 새로운 관측치가 생성된다. 이런 방식은 minority class에 변주를 주기 때문에 처음 지적했던 Oversampling의 단점을 보완하게 된다. 그림으로 간단하게 표현하면 다음과 같다.
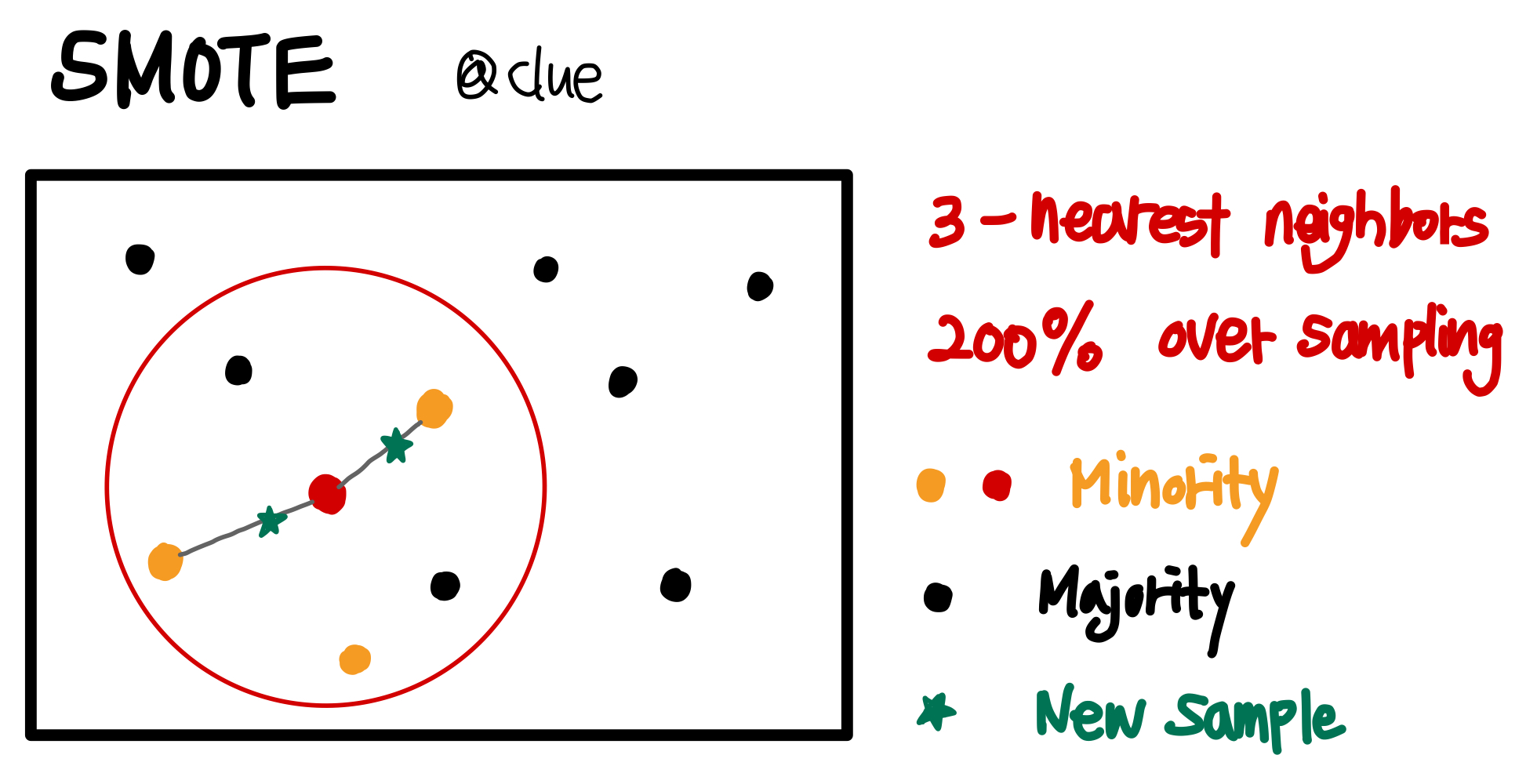
위는 SMOTE에 3-nearest neighbors 200% Oversampling를 적용하는 방식이다. 빨간색 점이 minority class라면 먼저 가장 가까운 3개의 다른 minority 관측치를 찾고 2배를 할 것이므로 두 점을 선택해서 linear 상의 랜덤한 초록색 별 위치를 새로운 샘플로 생성하는 것이다. 이를 모든 minority class에 이를 적용하면 된다. 일반적으로 SMOTE 후 모델링을 하면 성능을 향상시키지만 유일한 단점은 linear 상의 synthetic 샘플만 생성한다는 점이다.
다음은 Python으로 SMOTE를 수행하는 방법이다. 수행 후 원 데이터의 비율 2278:388에서 2278:2278가 되었다.
from imblearn.over_sampling import SMOTE
smote = SMOTE()
X_churn_sm, Y_churn_sm = smote.fit_resample(X_churn, Y_churn)2. ADASYN: Adaptive Synthetic Sampling Approach
기존의 SMOTE는 모든 minority class로부터 동일한 개수의 synthetic 샘플을 생성했지만, ADASYN은 각 관측치마다 생성하는 샘플의 수가 다르다는 점이 특징이다. 일종의 weight로 synthetic 샘플 수를 결정하고 이 weight는 knn 범위 내로 들어오는 majority class의 개수에 비례하도록 한다. 논문에서 이렇게 설정하는 이유는 더 훈련시키기 어려운 관측치에 집중하여 근방의 synthetic 샘플을 더 많이 생성하는 것이라고 설명한다. 즉, 한 minority class의 knn 내 majority 개수가 많다면 훈련 시 majority class와 비슷한 설명변수를 갖는 해당 minority class를 majority로 분류할 가능성이 높아질텐데, 더 많은 샘플을 생성함으로 해당 minority class가 무시되지 않도록 하는 것이라고 해석해볼 수 있겠다.
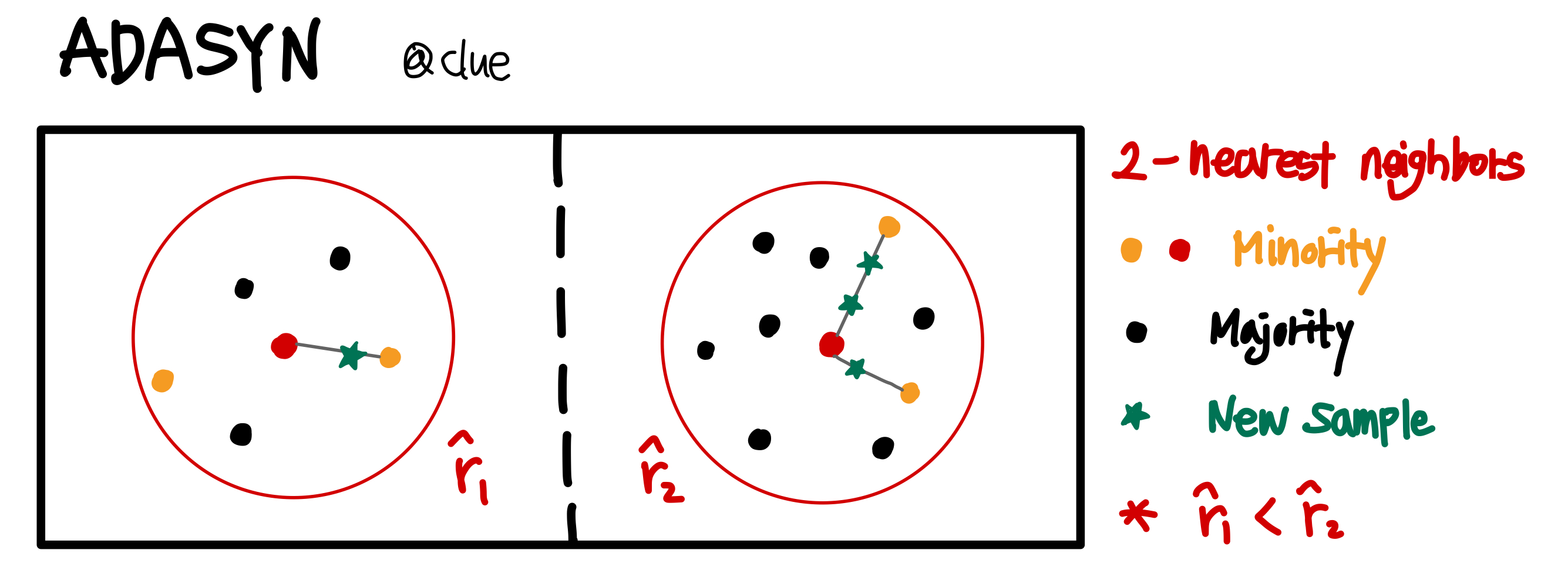
위는 k-nearest neighbors내 majority class 비율을 나타내는 ᴦ hat이 더 큰 경우에 더 많은 synthetic 샘플을 생성한다는 점을 그림으로 표현했다. 논문의 알고리즘을 보고 주관적으로 표현해본 것임을 참고하길 바란다.
다음은 Python으로 ADASYN을 수행하는 방법이다. 수행 후 원 데이터의 비율 2278:388에서 2278:2267가 되었다.
from imblearn.over_sampling import ADASYN
adasyn = ADASYN(random_state=22)
X_churn_ad, Y_churn_ad = adasyn.fit_resample(X_churn, Y_churn)3. SMOTE-Tomek
SMOTE-Tomek은 Oversampling과 Undersampling을 함께 수행하는 방법으로, 이름 그대로 SMOTE로 Oversampling을, Tomek Links로 Undersampling을 수행한다. Tomek Link는 두 샘플 A와 B가 있을 때, A의 nearest neighbor가 B이고(=B의 nearest neighbor가 A) A와 B가 다른 class에 속할 때를 의미하는데, 결국 Tomek Link를 찾고 majority class 샘플을 제외시키는 것이다. 이러한 방식으로 minority class와 가까운 majority class를 제외하면서 다소 모호할 수 있는 decision boundary가 명확히 구분될 수 있도록 한다.
Tomek Link Let d(x_i, x_j) denotes the Euclidean distance between x_i and x_j, where x_i denotes sample that belongs to the minority class and x_j denotes sample that belongs to the majority class. If there is no sample x_k satisfies the following condition:
- d(x_i, x_k) < d(x_i, x_j), or
- d(x_j, x_k) < d(x_i, x_j) then the pair of (x_i, x_j) is a Tomek Link.
SMOTE 수행 후 Tomek Link로 majority class를 제외한 것이 바로 SMOTE-Tomek이다. 아래의 그림은 Tomek Link를 나름대로 표현해본 그림이다.
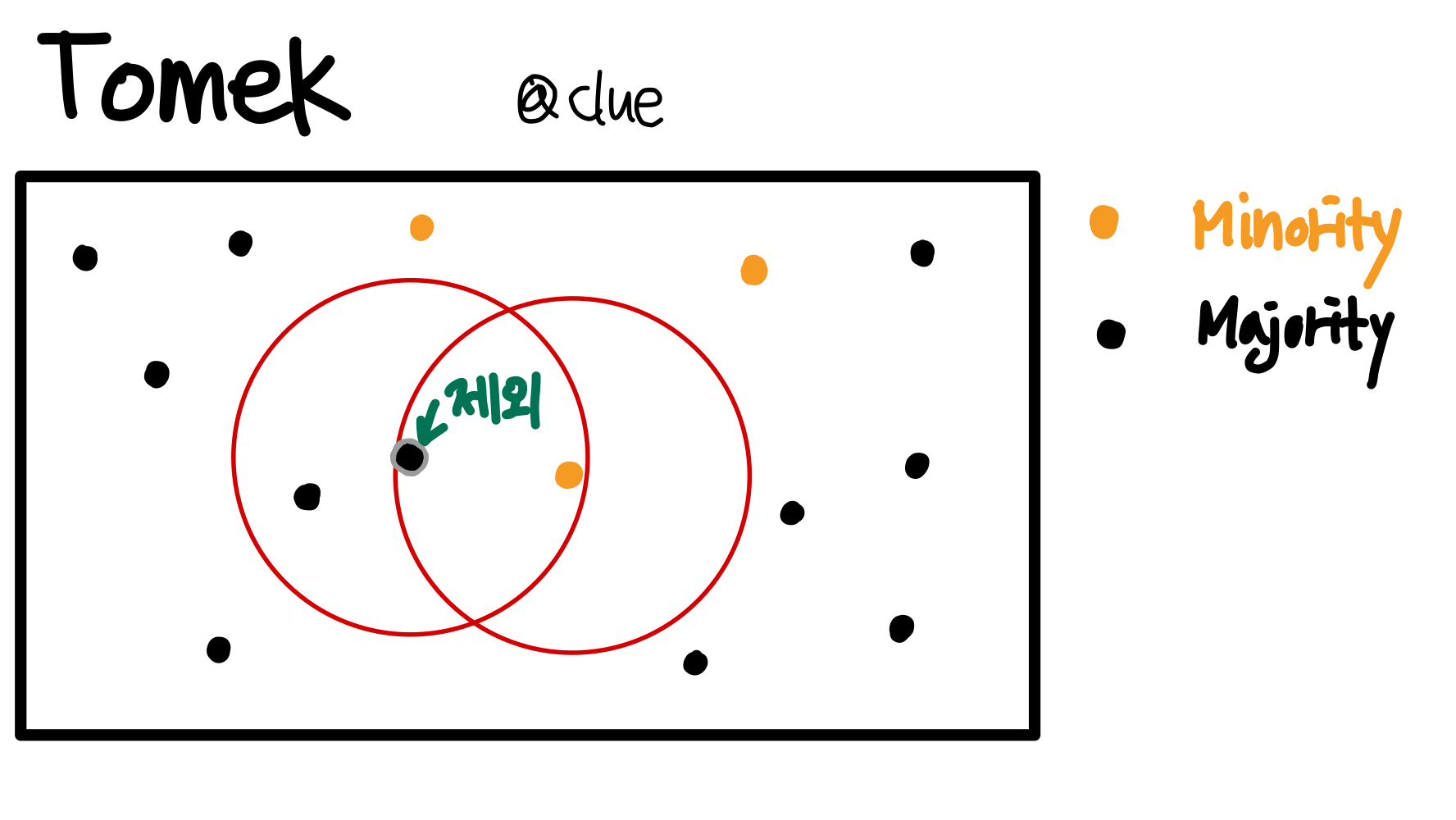
다음은 Python으로 SMOTE-Tomek을 수행하는 방법이다. 수행 후 원 데이터의 비율 2278:388에서 2270:2278가 되었다.
from imblearn.combine import SMOTETomek
from imblearn.under_sampling import TomekLinks
smoteto = SMOTETomek(tomek=TomekLinks(sampling_strategy='majority'))
X_churn_smt, Y_churn_smt = smoteto.fit_resample(X_churn, Y_churn)비교
앞에서 3가지 방법을 이용하여 고객 이탈 데이터를 평가한 결과는 다음과 같다. 간단한 전처리는 전처리는 이 페이지를 참고했으며 코드는 따로 첨부하지 않았다. 상대적으로 불균형에 강건한 부스팅 계열의 RandomForest를 사용했고 아무런 샘플링을 하지 않은 경우 3-Fold CV f1 score가 0.8097 정도이다. 세 가지 샘플링 방법 모두 수행 후 성능 향상이 일어났으며 그 중에서도 Oversampling과 Undersampling을 겸비한 SMOTE-Tomek의 성능이 가장 좋았다. 모두 동일한 다음의 코드로 모델링을 수행했으며 그 결과를 표로 첨부했다.
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.model_selection import cross_validate
rf=RandomForestClassifier(criterion='entropy')
cv_rf = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_validate(rf, X_churn_smt, Y_churn_smt, scoring='f1', cv=cv_rf, n_jobs=-1)
print('3-Fold CV f1 score: %.4f' % np.mean(scores['test_score']))| Number | Method | 3-fold CV f1 score |
|---|---|---|
| 0. | Original | 0.8097 |
| 1. | SMOTE | 0.9592 |
| 2. | ADASYN | 0.9584 |
| 3. | SMOTE-Tomek | 0.9593 |
